
- 1 2016•和平区一模)已知集合A={x||x﹣a|<1},B={x|1<x<4},则A∪B=B,则实数a的取值范围是( )
-
- A[2,3]
- B(2,3)
- C[0,5]
- D(0,5)
- 2 (2013•宁波模拟)设集合S={1,2,3,4,5,6,7,8,9},集合A={a1,a2,a3}是S的子集,且a1,a2,a3满足a1<a2<a3,a3﹣a2≤6,那么满足条件的集合A的个数为( )
-
- A78
- B76
- C84
- D83
【解析】
(1)列举法:
当a2=2时,3≤a3≤8,则a1=1,a3有6种取法,此时A有6个;
当a2=3时,4≤a3≤9,则a1有2种取法,a3有6种取法,此时A有12个;
当a2=4时,5≤a3≤9,则a1有3种取法,a3有5种取法,此时A有15个;
当a2=5时,6≤a3≤9,则a1有4种取法,a3有4种取法,此时A有16个;
当a2=6时,7≤a3≤9,则a1有5种取法,a3有3种取法,此时A有15个;
当a2=7时,8≤a3≤9,则a1有6种取法,a3有2种取法,此时A有12个;
当a2=8时,a3=9,则a1有7种取法,此时A有7个;
综上集合A的个数为6+12+15+16+15+12+7=83.故选D.
(2)组合法:
从集合S中任选3个元素组成集合A,一个能组成C93个,
其中A={1,2,9}不合条件,其它的都符合条件,
所以满足条件的集合A的个数C93﹣1=83.故选D
【答案】 D
- 3 (2015•湖北)已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为( )
-
- A77
- B49
- C45
- D30
【解析】
(1)列举法:
由题意可得,A={(0,0),(0,1),(0,﹣1),(1,0),(﹣1,0)},B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2)(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2)}.
根据定义A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},
可知A⊕B={(0,0),(0,1),(0,2),(0,﹣1),(0,﹣2),(1,0),(1,1),(1,2)(1,﹣1),(1,﹣2)(2,0),(2,1),(2,2),(2,﹣1),(2,﹣2),(﹣1,﹣2),(﹣1,﹣1),(﹣1,0),(﹣1,1),(﹣1,2),(﹣2,﹣2),(﹣2,﹣1),(﹣2,0),(﹣2,1),(﹣2,2), (﹣2,3),(﹣2,﹣3),(0,﹣3),(2,﹣3),(﹣1,3),(﹣1,﹣3),(1,3),(2,3),(0,3),(3,﹣1),(3,0)(3,1),(3,2),(3,﹣2)(﹣3,2)(﹣3,1),(1,﹣3),(﹣3,﹣1),(﹣3,0),(﹣3,﹣2)}共45个元素;
(2)图示法:
因为集合A={(x,y)|x2+y2≤1,x,y∈Z},所以集合A中有5个元素,即图中圆中的整点,B={(x,y)||x|≤2,|y|≤2,x,y∈Z},中有5×5=25个元素,即图中正方形ABCD中的整点,A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B}的元素可看作正方形A1B1C1D1中的整点(除去四个顶点),即7×7﹣4=45个.故选:C.
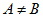
【答案】C

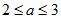 :,故选:A.
:,故选:A.