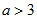立体教辅--针对薄弱环节的个性化辅导


- 1集合的含义:
-
一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合(简称为集)。
集合通常用大写的拉丁字母表示,如A、B、C、……元素通常用小写的拉丁字母表示,如a、b、c、……
- 4集合分类
-
根据集合所含元素个数不同,可把集合分为如下几类:
(1)把不含任何元素的集合叫做空集Ф
(2)含有有限个元素的集合叫做有限集
(3)含有无穷个元素的集合叫做无限集
- 5常用数集及其表示方法
-
(1)非负整数集(自然数集):全体非负整数的集合.记作N
(2)正整数集:非负整数集内排除0的集.记作N*或N+
(3)整数集:全体整数的集合.记作Z
(4)有理数集:全体有理数的集合.记作Q
(5)实数集:全体实数的集合.记作R
注:(1)自然数集包括数0.
(2)非负整数集内排除0的集.记作N*或N+,Q、Z、R等其它数集内排除0的集,也这样表示,例如,整数集内排除0的集,表示成Z*
- 6集合的表示方法

-
列举法:把集合中的元素一一列举出来,写在大括号内表示集合的方法.
描述法:用集合所含元素的共同特征表示集合的方法。具体方法是:在花括号内先写上表示这个集合元素的一般符号及取值范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征。
x
- 7集合间的关系
-
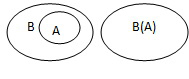
【注意】名称 自然语言描述 符号表示 Venn图表示 子集 如果集合A中所有元素都是集合B中的元素,则称集合A为集合B的子集 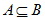
(或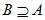 )
)
真子集 如果集合 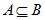 ,但存在元素
,但存在元素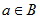 ,且
,且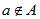 ,则称是结合的真子集
,则称是结合的真子集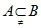
(或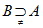 )
)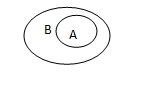
相等 集合A中的任一元素都是集合B中的元素,集合B中的任一元素也都是集合A中的元素,那么就是后所集合A与B集合相等 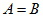
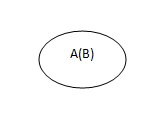
空集是任意集合的子集,是任意非空集合的真子集,符合表示
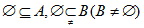

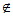 A
A
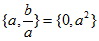 ,则下面正确的是( )
,则下面正确的是( )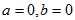
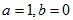
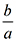 =0可知b=0,a=
=0可知b=0,a=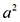 可知a=1。
可知a=1。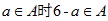 ,则a的值是( )
,则a的值是( )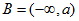 ,
,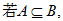 则a的取值范围为( )
则a的取值范围为( )